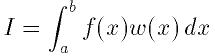
この章では1次元関数の数値積分(求積)を実行するルーチンについて述べる. 一般 の関数の適応的および非適応的積分ルーチンが実装されている. 無限領域および 半無限領域での積分, 対数特異点を含む特異点の積分, コーシー主値の計算, そ して振動積分も実装されている. このライブラリはQUADPACKで使われてい るPiessens, Doncker-Kapenga, Uberhuber, Kahanerにより実装された数値積分 パッケージを移植したものである. QUADPACKのFortranコードはNetlibで利 用できる.
この章で説明される関数はヘッダファイル`gsl_integration.h'で宣言され ている.
各アルゴリズムでは次の形の有界積分の近似値を計算する:
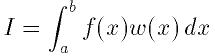
ここで
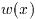 は重み関数(一般の被積分関数では
は重み関数(一般の被積分関数では
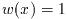 )である. ユーザーは次の精度要求を特定する相対誤差範囲
(epsabs, epsrel)を指定できる:
)である. ユーザーは次の精度要求を特定する相対誤差範囲
(epsabs, epsrel)を指定できる:
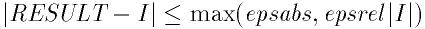
ここで
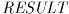 はアルゴリズムにより得られた数値的近似値である. アルゴリズムは絶対誤差
はアルゴリズムにより得られた数値的近似値である. アルゴリズムは絶対誤差
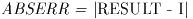 を次の不等式をみたす形で評価する:
を次の不等式をみたす形で評価する:
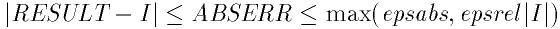
ルーチンは誤差範囲が厳密すぎると収束しなくなる. その場合途中で得られる最 良の近似値が返される.
QUADPACKにあるアルゴリズムは次のような名前付け規則に従っている:
Q- 求積ルーチンN- 非適応的積分A- 適応的積分G- 一般積分(ユーザー定義)W- 被積分関数に重みづけ関数をかけるS- 発散を含む積分P- 特異点を含む積分I- 無限範囲での積分O- cosまたはsinによる振動関数での重みづけF- フーリエ積分C- コーシー主値
アルゴリズムには, 高次および低次の規則による1対の積分則が使われている. 高次規則は狭い範囲の積分の近似値を計算するのに使われる. 高次および低次の 結果の差は近似の誤差評価に用いられる.
一般の(重みのない)関数の積分アルゴリズムはGauss-Kronrod則に基づいている. Gauss-Kronrod則はm次の古典的ガウス積分から始まる. これに 2m+1次の高次Kronrod則を与えるように横軸に点を付加する. Kornrod則 はガウス則で評価した関数値を再利用するので効果的である. 高次Kronrod則は 積分の最良近似値として用いられ, これら2つの規則の差は近似誤差として評価 される.
重み関数のある被積分関数の場合はClenshaw-Curtis求積法が用いられる. Clenshaw-Curtis則はn次Chebyschev多項式近似を被積分関数に適用する. この多項式は厳密に積分できるので, 元の被積分関数の積分近似値が求められる. Chebyschev展開は近似を改良するために高次に拡張することができる. 被積分関 数の特異点(や他の特徴)はChebyschev近似では収束を遅くする. QUADPACK で使われている改良Clenshaw-Curtis則は収束を遅くするいくつかの汎用重み関 数を分離している. これらの重み関数はChebyschev多項式に対して変形 Chebyschevモーメントとしてあらかじめ解析的に積分されている. このモーメ ントと関数のChebyschev近似を組みあわせることにより好きな積分を実行できる. 関数の特異部分に解析的積分を使うことで厳密に相殺することができ, 積分全体 の収束性をかなり改善できる.
QNGアルゴリズムは, 最大で87点で被積分関数のサンプリングを行う固定 Gauss-Kronrod則による非適応プロシージャである. これにより滑らかな関数を 高速に積分できる.
この関数は, (a,b)上のfの積分の近似値が要求される絶対および 相対誤差epsabsおよびepsrelの範囲内にある限り10点, 21点, 43点 および87点のGauss-Kronrod積分を実行する. この関数は最終的な近似値 result, 絶対誤差の見積りabserr, 用いられた関数評価数 nevalを返す. Gauss-Kronrod則は, 関数評価の総数を減らすため, 各段で 前段の結果を利用するよう設計されている.
QAGアルゴリズムは簡単な適応的積分プロシージャである. 積分区間を分割し,
各段で最大見積り誤差を与える区間を分割する. これにより全体の誤差が急減し,
区間の分割は被積分関数の局所的難点に集中することになる. この分割区間は
gsl_integration_workspace構造体で管理され, 区間, 結果, そして評価
誤差が格納される.
この関数はn個の倍精度の区間, 積分結果, 評価誤差を格納するのに十分 な作業空間を確保する.
この関数は作業空間wに割りあてられていたメモリを解放する.
この関数は(a,b)上のfの積分の近似値が要求される絶対および相 対誤差epsabsおよびepsrelの範囲内にある限り適応的に積分を実行 する. この関数は最終的な近似値result, 絶対誤差の評価値abserr を返す. 積分則はkeyの値により決定される. keyは次のシンボル名 から選ぶ:
GSL_INTEG_GAUSS15 (key = 1) GSL_INTEG_GAUSS21 (key = 2) GSL_INTEG_GAUSS31 (key = 3) GSL_INTEG_GAUSS41 (key = 4) GSL_INTEG_GAUSS51 (key = 5) GSL_INTEG_GAUSS61 (key = 6)
これは15, 21, 31, 41, 51, 61点Gauss-Kronrod則に相当する. 高次則は滑らか な関数であれば精度がよくなる. 低次則は不連続のような局所的難点を含む関数 で時間を節約できる.
積分の各段で, 適応的積分ストラテジに従い評価誤差が最大の区間を分割する. 区間分割とその結果はworkspaceで割りあてられるメモリに格納される. 区間分割数の最大値はlimitで与えられる. これは割りあてた作業領域の サイズを越えてはならない.
積分区間に可積分の特異点が存在すると, 適応的ルーチンの区間分割が特異点の まわりに集中してしまう. 分割された区間の幅が減少するとそれによる積分の近 似値は限られた形でしか収束しない. この収束を外挿により加速させる. QAGSア ルゴリズムは適応的区間分割にWynnεアルゴリズムを融合させ, 様々な可積分特 異点の積分をスピードアップさせる.
この関数は(a,b)上のfの積分の近似値が要求される絶対および相
対誤差epsabsおよびepsrelの範囲内にある限り21点Gauss-Kronrod
積分則を適応的に実行する. 結果は
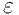 アルゴリズムにより外挿され, 不連続や可積分特異点の存在する積分の収束を加
速させる. この関数は外挿による最終近似値result, 絶対誤差の評価値
abserrを返す. 区間分割とその結果はworkspaceで割りあてられる
メモリに格納される. 分割区間の最大数はlimitで指定する. 作業空間の
割りあてサイズを越えてはならない.
アルゴリズムにより外挿され, 不連続や可積分特異点の存在する積分の収束を加
速させる. この関数は外挿による最終近似値result, 絶対誤差の評価値
abserrを返す. 区間分割とその結果はworkspaceで割りあてられる
メモリに格納される. 分割区間の最大数はlimitで指定する. 作業空間の
割りあてサイズを越えてはならない.
この関数はユーザーが提供する特異点の場所を考慮しながら適応的に積分を実行
するアルゴリズムQAGSの実装である. 長さnptsの配列ptsには積分
区間の端点と特異点の位置を格納する. 例えば, 区間(a,b)上で,
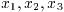 に特異点をもつ積分を実行する場合(ただし
に特異点をもつ積分を実行する場合(ただし
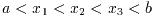 ), 次のようなpts配列を与える:
), 次のようなpts配列を与える:
pts[0] = a pts[1] = x_1 pts[2] = x_2 pts[3] = x_3 pts[4] = b
ここで npts = 5.
積分区間での特異点の位置を知っている場合は, このルーチンのほうが
QAGSより早い.
この関数は非有界区間
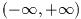 で関数fを積分する. 積分は変数変換
で関数fを積分する. 積分は変数変換
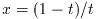 により区間
により区間
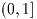 に写像される:
に写像される:
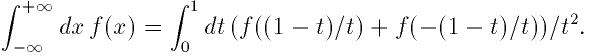
そしてQAGSアルゴリズムを用いて積分される. 変数変換により原点に可積分の特 異点ができてしまうので, 通常のQAGSの21点Gauss-Kronrod則を15点則におきか える. この場合低次則のほうがより効果的だからである.
この関数は半非有界区間
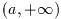 上で関数fを積分する. 積分は変数変換
上で関数fを積分する. 積分は変数変換
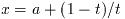 により区間
により区間
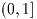 に写像される.
に写像される.
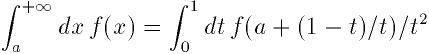
そしてQAGSアルゴリズムを用いて積分される.
この関数は半非有界区間
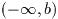 上で関数fを積分する. 積分は変数変換
上で関数fを積分する. 積分は変数変換
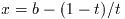 により区間
により区間
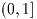 に写像される.
に写像される.
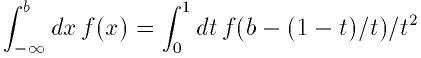
そしてQAGSアルゴリズムを用いて積分される.
この関数は
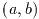 上のfの積分のcでの特異点のコーシー主値を求める.
上のfの積分のcでの特異点のコーシー主値を求める.
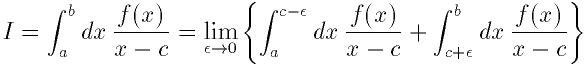
QAGの適応的分割アルゴリズムが使われるが, 特異点
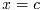 で分割されないように工夫されている. 分割区間が点
で分割されないように工夫されている. 分割区間が点
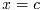 を含んでいたり, その点に近い場合は特別な25点変形Clenshaw-Curtis則が特異
点を避けるために使われる. 特異点から離れた場所では通常の15点
Gauss-Kronrod積分則が使われる.
を含んでいたり, その点に近い場合は特別な25点変形Clenshaw-Curtis則が特異
点を避けるために使われる. 特異点から離れた場所では通常の15点
Gauss-Kronrod積分則が使われる.
QAWSアルゴリズムは, 被積分関数が積分領域の端点で対数的な発散をするときに 用いられる. 効果的に計算するため, Chebyschevモーメントをあらかじめ計算し ておく.
この関数はgsl_integration_gaws_tableの領域を確保し, 特異点の重み
関数
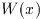 をパラメータ
をパラメータ
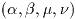 で表現するための作業領域を割りあてる:
で表現するための作業領域を割りあてる:
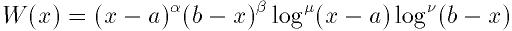
ここで
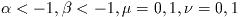 である. 重み関数は
である. 重み関数は
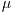 ,
, 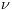 の値により以下の4つの形をとる:
の値により以下の4つの形をとる:
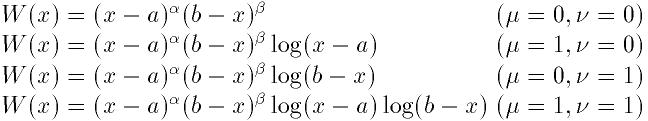
特異点
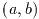 は積分が計算されるまで特定されなくてもよい. これらは積分領域の端点である.
は積分が計算されるまで特定されなくてもよい. これらは積分領域の端点である.
この関数は, エラーが検出されなければ, 新しく割りあてられた
gsl_integration_qaws_tableへのポインタを返す. エラーの場合には0を
返す.
gsl_integration_qaws_table構造体tのパラメータ
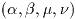 を変更する.
を変更する.
gsl_integration_qaws_table構造体tに割りあてられた
メモリを解放する.
この関数は特異点重み関数
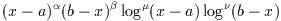 を用いて区間
を用いて区間
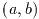 上で関数f(x)を積分する. パラメータ
上で関数f(x)を積分する. パラメータ
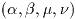 はテーブルtから取得する.
はテーブルtから取得する.
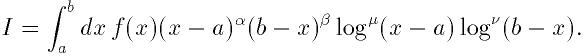
QAGの適応的分割アルゴリズムが用いられる. 分割区間に端点が含まれるときは 特殊25点変形Clenshaw-Curtis則が特異点を避けるために用いられる. 端点を含 まない区間では通常の15点Gauss-Kronrod則が用いられる.
QAWOアルゴリズムは振動因子
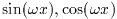 をもつ積分を計算する. 効果的に計算するため, この因子をあらかじめ計算した
Chebyschevモーメントのテーブルが必要となる.
をもつ積分を計算する. 効果的に計算するため, この因子をあらかじめ計算した
Chebyschevモーメントのテーブルが必要となる.
この関数はgsl_integration_qawo_table構造体のために空間を割りあて,
パラメータ
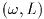 をもつサインまたはコサインの重み関数
をもつサインまたはコサインの重み関数
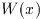 のための作業領域となる.
のための作業領域となる.
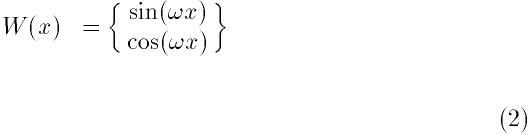
パラメータLは関数の積分領域の長さ
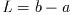 を与える. サインかコサインの選択はパラメータsineで行われる. 値には
以下のシンボル値を用いる:
を与える. サインかコサインの選択はパラメータsineで行われる. 値には
以下のシンボル値を用いる:
GSL_INTEG_COSINE GSL_INTEG_SINE
gsl_integration_qawo_tableは積分過程で必要となる三角関数表である.
パラメータnにより計算される係数のレベルが指定される. 各レベルは間
隔Lの分割に相当するので, nレベルは長さ
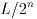 までの分割区間に対応できる. 積分ルーチン
までの分割区間に対応できる. 積分ルーチンgsl_integration_qawoは,
要求された精度に対してレベル数が不足している場合にはGSL_ETABLEを
返す.
この関数は, テーブルwfで定義される重み関数
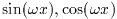 を用い, 区間
を用い, 区間
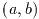 上で関数fの積分を計算する適応的アルゴリズムである.
上で関数fの積分を計算する適応的アルゴリズムである.
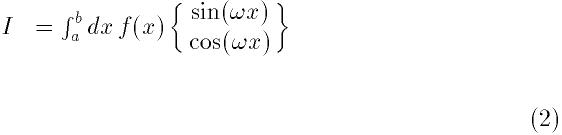
積分の収束加速するため, 結果は
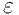 アルゴリズムを用いて外挿される. 関数は最終的な推定値result, 絶対誤
差の評価値abserrを返す. 分割区間とその結果はworkspaceのメモ
リに格納される. 分割区間の最大数はlimitで与えられる. これは作業領
域の割りあてサイズを越えてはならない.
アルゴリズムを用いて外挿される. 関数は最終的な推定値result, 絶対誤
差の評価値abserrを返す. 分割区間とその結果はworkspaceのメモ
リに格納される. 分割区間の最大数はlimitで与えられる. これは作業領
域の割りあてサイズを越えてはならない.
「大きな」幅
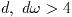 をもつ分割区間は25点Clenshaw-Curtis積分則を用いて計算し, 振動を処理する.
「小さな」幅
をもつ分割区間は25点Clenshaw-Curtis積分則を用いて計算し, 振動を処理する.
「小さな」幅
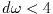 をもつ分割区間では15点Gauss-Kronrod積分を用いる.
をもつ分割区間では15点Gauss-Kronrod積分を用いる.
この関数は半非有界区間
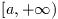 での関数fのFourier積分を計算する.
での関数fのFourier積分を計算する.
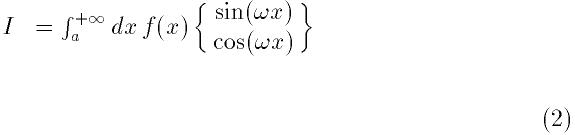
パラメータ
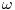 はテーブルwf(長さLは好きな値をとることができる. Fourier積分
に適切な値となるようにこの関数によりオーバーライドされるからである)から
とられる. 積分はQAWOアルゴリズムを使って各分割区間で計算される.
はテーブルwf(長さLは好きな値をとることができる. Fourier積分
に適切な値となるようにこの関数によりオーバーライドされるからである)から
とられる. 積分はQAWOアルゴリズムを使って各分割区間で計算される.
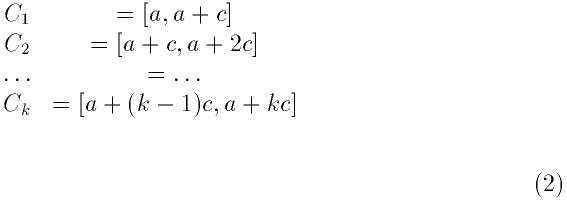
ここで
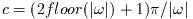 は周期の奇数倍をカバーするように選ばれる. 各区間からの寄与は符号が交代し,
fが正で単調減少する場合には単調減少する. この数列の和は
は周期の奇数倍をカバーするように選ばれる. 各区間からの寄与は符号が交代し,
fが正で単調減少する場合には単調減少する. この数列の和は
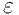 アルゴリズムで加速する.
アルゴリズムで加速する.
この関数は全体の絶対誤差abserrで押さえられる. 以下のストラテジが用
いられる: 各区間
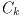 でアルゴリズムは許容誤差を達成しようとする:
でアルゴリズムは許容誤差を達成しようとする:
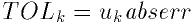
ここで
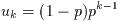 および
および
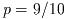 である. 各区間の三角関数列の寄与の和は全体の許容誤差abserrを与える.
である. 各区間の三角関数列の寄与の和は全体の許容誤差abserrを与える.
分割区間の積分に困難が発生した場合は分割区間に対する精度要求を緩和する.
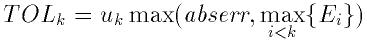
ここで
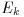 は区間
は区間
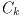 での評価誤差である.
での評価誤差である.
分割区間とその結果はworkspaceのメモリに格納される. 分割区間の最大 数はlimitで与えられる. 作業領域の割りあてサイズより大きくなくては ならない. 各分割区間での積分にはcycle_workspaceのメモリがQAWOアル ゴリズムのための作業領域として用いられる.
不正引数に関する標準エラーコードの他, これらの関数は次の値を返す:
GSL_EMAXITER
GSL_EROUND
GSL_ESING
GSL_EDIVERGE
積分ルーチンQAGSは有界積分の大くのクラスで計算できる. 例えば, 次
のような積分を考える. これは原点に対数的な特異点をもつ:
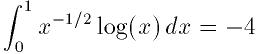
以下のプログラムはこの積分を相対誤差1e-7で積分するものである.
#include <stdio.h>
#include <math.h>
#include <gsl/gsl_integration.h>
double f (double x, void * params) {
double alpha = *(double *) params;
double f = log(alpha*x) / sqrt(x);
return f;
}
int
main (void)
{
gsl_integration_workspace * w
= gsl_integration_workspace_alloc(1000);
double result, error;
double expected = -4.0;
double alpha = 1.0;
gsl_function F;
F.function = &f;
F.params = α
gsl_integration_qags (&F, 0, 1, 0, 1e-7, 1000,
w, &result, &error);
printf("result = % .18f\n", result);
printf("exact result = % .18f\n", expected);
printf("estimated error = % .18f\n", error);
printf("actual error = % .18f\n", result - expected);
printf("intervals = %d\n", w->size);
return 0;
}
以下に示す結果は, 8回分割することにより望んだ精度が達成できたことを示し ている.
bash$ ./a.out result = -3.999999999999973799 exact result = -4.000000000000000000 estimated error = 0.000000000000246025 actual error = 0.000000000000026201 intervals = 8
実際, QAGSで用いられる外挿プロシージャは要求精度の倍近い精度をも
つ. 外挿プロシージャの返す評価誤差は実際の誤差よりも大きい. 安全のため1
桁のマージンをとっているからである.
以下の本はQUADPACKの参考書の決定版であり, 作者により書かれたもので ある. アルゴリズム, プログラム一覧, テストプログラム, そして例題が載せら れている. 数値積分に関する有用なアドバイスや, QUADPACKの開発に用い られた数値積分に関する参考書も載せれている.
This document was generated on 8 November 2001 using texi2html 1.56k.