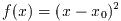や
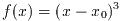のような). 偶数次の重解に対しては囲い込み法は使えない. これらの方法では,
初期範囲は0をよぎらなければならない. つまり両端点で片方は正, もう片方は
負の値をとらなければならない. 偶数次の重解は0をよぎらず, 接するだけであ
る. 囲い込み法は奇数次の重解(3次, 5次...)では機能する. 解の洗練法は
一般的に高次の重解を探査することができるが, 収束が悪くなる. この場合収束
の加速にSteffensonアルゴリズムを用いるとよい.
この章では任意の1次元関数の解を探索するルーチンについて述べる. このライ ブラリは様々な反復的解探査と収束テストの低レベルのコンポーネントを実装し ている. これらをユーザーが組みあわせて, 反復の途中段階すべてを見て望まし い解を得ることができる. メソッドの各クラスで同じ枠組が使われているので, プログラムを再コンパイルせずに実行時に解法を切り替えることができる. 解法 の各インスタンスで状態を保持しているので, マルチスレッドプログラムでも使 うことができる.
ヘッダファイル`gsl_roots.h'に解探査関数のプロトタイプと関連する定義 がある.
1次元解探査アルゴリズムは2つのクラスに分けることができる. 解の囲い 込みと解の洗練である. 解を囲い込むアルゴリズムは収束を保証できる. 囲い込みアルゴリズムは解のあることを知っている区間が出発点となる. 区間の 幅は反復的に縮小され, 望む許容誤差以下に区間幅が縮小するまで探査が続く. これは解の位置の誤差評価が厳密に行える利点がある.
解の洗練の技法は, 解の初期推測値を改良しようとする. このアルゴリズ ムは解に「十分近い」出発点を与えたときのみ収束する. またスピードのため厳 密な誤差評価を犠牲にする. 解近傍で関数の挙動を近似することで, 初期値の高 次の改良を試みる. 関数の挙動がアルゴリズムのものに近く, 初期値がよく推定 できる時には洗練アルゴリズムは素早く収束する.
GSL ではどちらのタイプのアルゴリズムも同じ枠組みに収めた. ユーザーはアル ゴリズムの高レベルドライバを実装し, ライブラリは各ステップに必要な個々の 関数を実装する. 反復には3つのメインフェーズが存在する:
囲い込み法の状態はgsl_root_fsolver構造体に保持される. 更新プロシー
ジャは関数値のみ用いる(導関数値は用いない). 洗練法の状態は
gsl_root_fdfsolver構造体に保持される. 更新には関数とその導関数が
必要となる(このためfdfという名前になっている).
解探査関数は1度に1つの解しか探査しない. 探査領域内にいくつかの解があると き, 始めに見付かった解を返す. しかしどの解が見付かったのかを調べるのは難 しい. 多くの場合, 複数の解がある領域で解を探している場合にも何も警 告されない.
重解を持つ関数の取り扱いには注意を要する(たとえば
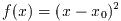や
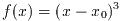のような). 偶数次の重解に対しては囲い込み法は使えない. これらの方法では,
初期範囲は0をよぎらなければならない. つまり両端点で片方は正, もう片方は
負の値をとらなければならない. 偶数次の重解は0をよぎらず, 接するだけであ
る. 囲い込み法は奇数次の重解(3次, 5次...)では機能する. 解の洗練法は
一般的に高次の重解を探査することができるが, 収束が悪くなる. この場合収束
の加速にSteffensonアルゴリズムを用いるとよい.
探査領域に
が解を持つことは絶対必要というわけではないが, 解の存在を調べるの
に数値解探査関数を使うべきではない. もっとよい方法がある. 数値解探査が間
違う可能性があるのだから, よく知らない関数を丸投げするのはよくない. 一般
的に解を探す前にグラフを描いてチェックするのがよいだろう.
この関数はタイプTのソルバのインスタンスを新しく割りあててポインタ を返す. 例えば, 次のコードはbisectionソルバのインスタンスを作成する:
const gsl_root_fsolver_type * T = gsl_root_fsolver_bisection; gsl_root_fsolver * s = gsl_root_fsolver_alloc (T);
ソルバを作るのに十分なメモリがない場合, 関数はヌルポインタを返し, エラー
コードGSL_ENOMEMによりエラーハンドラが呼びだされる.
この関数はタイプTの導関数ベースのソルバのインスタンスを新しく割り あててポインタを返す. 例えば, 次のコードはNewton-Raphsonソルバのインスタ ンスを作成する:
const gsl_root_fdfsolver_type * T = gsl_root_fdfsolver_newton; gsl_root_fdfsolver * s = gsl_root_fdfsolver_alloc (T);
ソルバを作るのに十分なメモリがない場合, 関数はヌルポインタを返し, エラー
コードGSL_ENOMEMによりエラーハンドラが呼びだされる.
この関数は存在するソルバsが関数fの解を初期探査範囲 [x_lower, x_upper]で探査するよう(再)初期化する.
この関数は存在するソルバsが関数とその微分fdfおよび初期値 rootで探査するように(再)初期化する.
この関数はソルバsに割りあてられたメモリを解放する.
これらの関数はソルバの名前のポインタを返す. 例えば
printf("s is a '%s' solver\n",
gsl_root_fsolver_name (s)) ;
は, s is a 'bisection' solverのような出力を返す.
解探査をさせるため, 1変数の連続関数, および場合によりその導関数を与える 必要がある. 一般のパラメータを許すため, 関数は次のデータ型で定義されてい る必要がある:
double (* function) (double x, void * params)
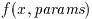を返す.
void * params
一般の2次関数を例にあげる:
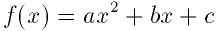
ここで
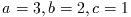だとしよう. 次のコードは解探査が可能な関数gsl_function Fを
定義する:
struct my_f_params { double a; double b; double c; } ;
double
my_f (double x, void * p) {
struct my_f_params * params
= (struct my_f_params *)p;
double a = (params->a);
double b = (params->b);
double c = (params->c);
return (a * x + b) * x + c;
}
gsl_function F;
struct my_f_params params = { 3.0, 2.0, 1.0 };
F.function = &my_f;
F.params = ¶ms;
関数
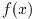は次のマクロにより評価できる：
#define GSL_FN_EVAL(F,x)
(*((F)->function))(x,(F)->params)
double (* f) (double x, void * params)
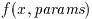を返す.
double (* df) (double x, void * params)
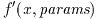を返す.
void (* fdf) (double x, void * params, double * f, double * df)
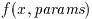に, そして導関数dfの値を
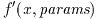で求めることを宣言する. この関数は別々の関数
, 
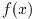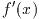を最適化する--関数値とその導関数値を同時に求めることにより高速化を図って
いる.
void * params
次の関数を例に挙げる:
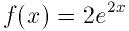
double
my_f (double x, void * params)
{
return exp (2 * x);
}
double
my_df (double x, void * params)
{
return 2 * exp (2 * x);
}
void
my_fdf (double x, void * params,
double * f, double * df)
{
double t = exp (2 * x);
*f = t;
*df = 2 * t; /* computing using existing values */
}
gsl_function_fdf FDF;
FDF.f = &my_f;
FDF.df = &my_df;
FDF.fdf = &my_fdf;
FDF.params = 0;
関数
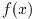は次のマクロで評価できる:
#define GSL_FN_FDF_EVAL_F(FDF,x)
(*((FDF)->f))(x,(FDF)->params)
導関数
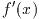は次のマクロで評価できる:
#define GSL_FN_FDF_EVAL_DF(FDF,x)
(*((FDF)->df))(x,(FDF)->params)
そして関数値
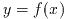および導関数値
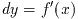を同時に求めるには次のマクロを使う:
#define GSL_FN_FDF_EVAL_F_DF(FDF,x,y,dy)
(*((FDF)->fdf))(x,(FDF)->params,(y),(dy))
このマクロは
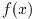をyに, そして
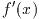をdyに格納する---これらはともにdouble型のポインタである.
ユーザーは初期範囲か初期値を与えることになる. この章では探査範囲や推定値 がどのように機能し, 関数の引数がどのようにそれらを制御するのかを解説する.
推定値は単にxの値である. 解に対して許容範囲内に近づくまで反復され
る. double型をもつ.
探査範囲は区間の両端点である. 区間幅が要求精度内になるまで反復される. 区 間は上限と下限を示す2つの値で指定される. 端点を区間に含むかどうかは区間 の使われる状況による.
以下の関数は各アルゴリズムでの反復を制御する. 各関数は相当する型のソルバ の状態を更新する反復を1回行う. 同じ関数であらゆるソルバに対応するため, コードを変更することなく実行時にメソッドを変更することができる.
GSL_EBADFUNC
InfまたはNaNとなる特異点が発生した.
GSL_EZERODIV
ソルバはその時点での解の最も良い推定値を保持している. 囲い込み法ではその 時点で最も良い解区間を保持している. この情報は次の関数で参照することがで きる:
解探査プロシージャは以下の条件が真になったときに停止する:
これらの条件の処理はユーザーに任せられている. 以下の関数はユーザーが標準 的な方法により現在の結果の精度を調べるために用意されている.
GSL_SUCCESSを返す.
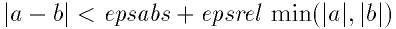
ただし, 区間
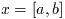が原点を含んでいないことが必要である. 原点を含んでいる場合には
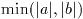は(区間の最小値である)0に置きかえられる. これは原点近くの解での相対誤差
の正確な評価に必要な操作である.
区間に対するこの条件により, 区間内の推定値rが真の解 r* に対して同様の条件を満たすことを要請する:
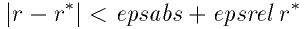
ただし区間内に真の解が存在すると仮定している.
GSL_SUCCESSを返す:
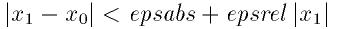
満たされていない場合にはGSL_CONTINUEを返す.
GSL_SUCCESSを返す:
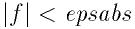
満たされない場合はGSL_CONTINUEを返す. この条件は残差|f(x)|
が十分小さいため, 真の解xの正確な場所が重要でなくなる場合には適し
ている.
この章で説明する解の囲い込み法は解が含まれていることを知っている初期範囲 が必要となる--aとbが範囲の端点であれば, f(a)と f(b)は符号が異なる必要がある. つまり与えられた区間で少なくとも1回 は0をよぎる必要がある. 妥当な初期範囲が与えられれば, 関数の振舞いがよけ ればこれらのアルゴリズムは失敗することはない.
囲い込み法では偶数次の重解は見つけることができない. x軸に接するか らである.
2分法は囲い込み法のうち最も簡単な方法である. 線型収束を示し, ライ ブラリ中で最も遅く収束するアルゴリズムである.
各段で, 区間は2等分され, 中点での関数値が求められる. この値の符号により どちらの区間に解が含まれるかを決定する. 区間の半分が捨てられ残る半分が新 しい推定区間となる. このプロシージャが, 区間幅が十分小さくなるまで繰り返 される.
どの時点でも, 解の推定値は中点の値である.
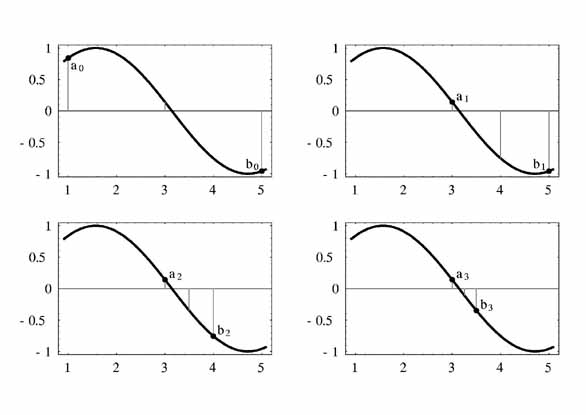
2分法を4回繰り返した. a_nは区間始点のn番目の位置, b_nは区間終点のn番目の位置. 各段での中点の位置も示してある.
false position アルゴリズムは線型補完による解探査法である. 収束は 線型だが, 一般に2分法より早い.
各段で, 端点(a,f(a)), (b,f(b))を結ぶ直線が引かれ, x 軸との交点を「中点」とする. この点での関数値が計算され, その符号でどちら の領域を採用するかを決定し, 片方を捨て残りを次の領域とする. このプロシー ジャが区間が十分に小さくなるまで繰り返される.
現在の推定値は線型補完により求められる.
Brent-Dekker法(Brent法と略すことにする)は2分法アルゴリズムと 内挿を組みあわせたものである. この方法は荒っぽいが早いアルゴリズムである.
各段でBrent法は内挿曲線で関数を近似する. 初段では2端点の直線近似だが, 段 が進むにつれ 最新の3点について逆2乗フィットを行う. 内挿曲線とx軸 の交点を解の推定値とする. 推定値が現在の推定区間にある場合は内挿点を用い, 区間を縮小する. 内挿点が求められない時は通常の2分法に切りかえる.
最新の推定値は最新の内挿もしくは2分法の値である.
この章で説明する解の洗練法は解の位置をあらかじめ推定しておく必要がある. 収束するという絶対的な保証はない--関数はこの手法に適した形をしていなくて はならず, 初期値は真の解に十分近くなければならない. 条件が満たされたとき には収束は2次である.
これらのアルゴリズムは関数とその導関数が必要となる.
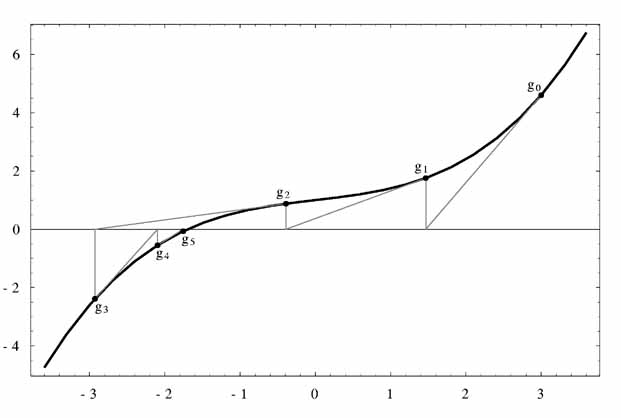
Newton法は標準的な解洗練アルゴリズムである. このアルゴリズムは解の位置の 初期推定値から始まる. 各段で, 関数fの接線がひかれる. 接線と x軸の交点が新しい推定値となる. 繰り返しは次の数列で定義される:
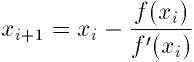
Newton法は単一の解に対しては2次で, 複数の解には線型で収束する.
Newton法での数回の繰り返し. g_nはn番目の推定値である.
割線法はNewton法を単純化したもので, 導関数を毎回求める必要がない.
初段ではアルゴリズムはNewton法から始め, 導関数を用いる.
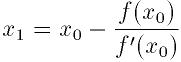
続く繰り返しでは, 微分値を求める代わりに数値的な推定値で代用する. 前の2 点の傾きを使うことになる:
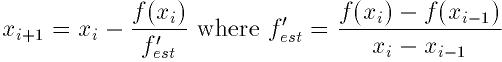
導関数が解の近傍でさほど変化しないときには, 割線法はかなりの省力化を図る ことができる. 導関数の評価が関数自身の評価よりコストが0.44倍以上かかるの であれば, 割線法はニュートン法より早い. 数値微分の計算と同様, 2点の間隔 が小さくなりすぎると桁落ちが生じる.
単一の解であれば, 収束は
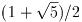(約1.62)次である. 複数の解では線型で収束する.
Steffenson法はこれらルーチンの中で最も早い収束を示す. これは基本的 なNewton法にAitkenの「デルタ2乗」加速を組みあわせたものである. Newton法 の各段をx_iとしたとき, 加速により新しい数列R_iを生成する:
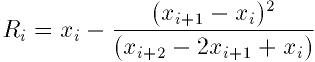
これは合理的な条件のもとで元の数列よりも早く収束する. 加速数列を生成する には最低3項必要である. 初段では元のNewton法の結果を返す. 加速項の分母が0 になる場合もNewton法の結果を返す.
加速プロシージャを用いているため, 関数の振舞いが悪い場合にはこの方法は不 安定になる.
どの解探査法であっても, 解くべき方程式を用意する必要がある. この例では, 前に示した一般の2次方程式を解くことにしよう. まず関数のパラメータを定義 するためにヘッダファイル(`demo_fn.h')が必要である.
struct quadratic_params
{
double a, b, c;
};
double quadratic (double x, void *params);
double quadratic_deriv (double x, void *params);
void quadratic_fdf (double x, void *params,
double *y, double *dy);
関数の定義は別のファイル(`demo_fn.c')で行うことにしよう.
double
quadratic (double x, void *params)
{
struct quadratic_params *p
= (struct quadratic_params *) params;
double a = p->a;
double b = p->b;
double c = p->c;
return (a * x + b) * x + c;
}
double
quadratic_deriv (double x, void *params)
{
struct quadratic_params *p
= (struct quadratic_params *) params;
double a = p->a;
double b = p->b;
double c = p->c;
return 2.0 * a * x + b;
}
void
quadratic_fdf (double x, void *params,
double *y, double *dy)
{
struct quadratic_params *p
= (struct quadratic_params *) params;
double a = p->a;
double b = p->b;
double c = p->c;
*y = (a * x + b) * x + c;
*dy = 2.0 * a * x + b;
}
最初のプログラムはBrent法のソルバgsl_root_fsolver_brentを用い, 次
の方程式を解くものである.
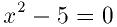
この解は
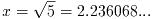である.
#include <stdio.h>
#include <gsl/gsl_errno.h>
#include <gsl/gsl_math.h>
#include <gsl/gsl_roots.h>
#include "demo_fn.h"
#include "demo_fn.c"
int
main (void)
{
int status;
int iter = 0, max_iter = 100;
const gsl_root_fsolver_type *T;
gsl_root_fsolver *s;
double r = 0, r_expected = sqrt (5.0);
double x_lo = 0.0, x_hi = 5.0;
gsl_function F;
struct quadratic_params params = {1.0, 0.0, -5.0};
F.function = &quadratic;
F.params = ¶ms;
T = gsl_root_fsolver_brent;
s = gsl_root_fsolver_alloc (T);
gsl_root_fsolver_set (s, &F, x_lo, x_hi);
printf ("using %s method\n",
gsl_root_fsolver_name (s));
printf ("%5s [%9s, %9s] %9s %10s %9s\n",
"iter", "lower", "upper", "root",
"err", "err(est)");
do
{
iter++;
status = gsl_root_fsolver_iterate (s);
r = gsl_root_fsolver_root (s);
x_lo = gsl_root_fsolver_x_lower (s);
x_hi = gsl_root_fsolver_x_upper (s);
status = gsl_root_test_interval (x_lo, x_hi,
0, 0.001);
if (status == GSL_SUCCESS)
printf ("Converged:\n");
printf ("%5d [%.7f, %.7f] %.7f %+.7f %.7f\n",
iter, x_lo, x_hi,
r, r - r_expected,
x_hi - x_lo);
}
while (status == GSL_CONTINUE && iter < max_iter);
return status;
}
以下に結果を挙げる:
bash$ ./a.out
using brent method
iter [ lower, upper] root err err(est)
1 [1.0000000, 5.0000000] 1.0000000 -1.2360680 4.0000000
2 [1.0000000, 3.0000000] 3.0000000 +0.7639320 2.0000000
3 [2.0000000, 3.0000000] 2.0000000 -0.2360680 1.0000000
4 [2.2000000, 3.0000000] 2.2000000 -0.0360680 0.8000000
5 [2.2000000, 2.2366300] 2.2366300 +0.0005621 0.0366300
Converged:
6 [2.2360634, 2.2366300] 2.2360634 -0.0000046 0.0005666
Brent法ではなく2分法を使うようにする場合は,
gsl_root_fsolver_brentをgsl_root_fsolver_bisectionに変更す
ればよい. この場合, 収束が遅くなる:
bash$ ./a.out
using bisection method
iter [ lower, upper] root err err(est)
1 [0.0000000, 2.5000000] 1.2500000 -0.9860680 2.5000000
2 [1.2500000, 2.5000000] 1.8750000 -0.3610680 1.2500000
3 [1.8750000, 2.5000000] 2.1875000 -0.0485680 0.6250000
4 [2.1875000, 2.5000000] 2.3437500 +0.1076820 0.3125000
5 [2.1875000, 2.3437500] 2.2656250 +0.0295570 0.1562500
6 [2.1875000, 2.2656250] 2.2265625 -0.0095055 0.0781250
7 [2.2265625, 2.2656250] 2.2460938 +0.0100258 0.0390625
8 [2.2265625, 2.2460938] 2.2363281 +0.0002601 0.0195312
9 [2.2265625, 2.2363281] 2.2314453 -0.0046227 0.0097656
10 [2.2314453, 2.2363281] 2.2338867 -0.0021813 0.0048828
11 [2.2338867, 2.2363281] 2.2351074 -0.0009606 0.0024414
Converged:
12 [2.2351074, 2.2363281] 2.2357178 -0.0003502 0.0012207
次のプログラムは同じ関数を導関数も用いて解を探査するものである.
#include <stdio.h>
#include <gsl/gsl_errno.h>
#include <gsl/gsl_math.h>
#include <gsl/gsl_roots.h>
#include "demo_fn.h"
#include "demo_fn.c"
int
main (void)
{
int status;
int iter = 0, max_iter = 100;
const gsl_root_fdfsolver_type *T;
gsl_root_fdfsolver *s;
double x0, x = 5.0, r_expected = sqrt (5.0);
gsl_function_fdf FDF;
struct quadratic_params params = {1.0, 0.0, -5.0};
FDF.f = &quadratic;
FDF.df = &quadratic_deriv;
FDF.fdf = &quadratic_fdf;
FDF.params = ¶ms;
T = gsl_root_fdfsolver_newton;
s = gsl_root_fdfsolver_alloc (T);
gsl_root_fdfsolver_set (s, &FDF, x);
printf ("using %s method\n",
gsl_root_fdfsolver_name (s));
printf ("%-5s %10s %10s %10s\n",
"iter", "root", "err", "err(est)");
do
{
iter++;
status = gsl_root_fdfsolver_iterate (s);
x0 = x;
x = gsl_root_fdfsolver_root (s);
status = gsl_root_test_delta (x, x0, 0, 1e-3);
if (status == GSL_SUCCESS)
printf ("Converged:\n");
printf ("%5d %10.7f %+10.7f %10.7f\n",
iter, x, x - r_expected, x - x0);
}
while (status == GSL_CONTINUE && iter < max_iter);
return status;
}
Newton法の結果を以下に挙げる:
bash$ ./a.out
using newton method
iter root err err(est)
1 3.0000000 +0.7639320 -2.0000000
2 2.3333333 +0.0972654 -0.6666667
3 2.2380952 +0.0020273 -0.0952381
Converged:
4 2.2360689 +0.0000009 -0.0020263
誤差は前の段との差を取るより次の段との差をとる方がより正確となる.
gsl_root_fdfsolver_newtonをgsl_root_fdfsolver_secantや
gsl_root_fdfsolver_steffensonに変えることで他の方法に切りかえるこ
とができる.
Brent-Dekkerアルゴリズムについては以下の2つの論文を参照すること.
This document was generated on 8 November 2001 using texi2html 1.56k.